Använd vår kalkylator för att beräkna ränta på ränta effekten.
Fyll i kalkylatorn med ditt månadsparande, förväntad årsavkastning samt hur många år du vill räkna med och klicka på ”beräkna ränta på ränta”. Du får då både en graf och en tabell som tydligt och pedagogiskt visar utvecklingen på det investerade kapitalet. Lite längre ner på sidan kan du läsa om vad ränta-på-ränta-effekten är, hur den beräknas och hur du kan uppnå den.
Kalkylator
💡 Erbjudanden – gratis courtage vid aktiehandel!
🔗 Levler.se | Ny svensk nätmäklare med 0 kr i courtage för alla fram till 2025-03-31.
🔗 Avanza.se | 0 kr i courtage & fondavgifter för alla med max 50 000 kr på kontot.
🔗 Nordnet.se | 0 kr i courtage & fondavgifter för alla med max 50 000 kr på kontot.
Dela upp dina pengar på olika nätmäklare för att handla med gratis courtage för en större summa.
Det är gratis att öppna och att ha konto hos alla nätmäklarna ovan.
Gratis courtage:
Courtage är namnet på avgiften som nätmäklarna tar vid köp- och sälj av aktier. Nätmäklarna ovan erbjuder gratis courtage vid aktiehandel vilket innebär att du inte behöver betala någon avgift när du köper och säljer så länge du uppfyller kraven för erbjudandet.
Gratis fondavgifter:
Avanza och Nordnet erbjuder 0 kr i fondavgifter så länge du har max 50 000 kr på kontot. Fondavgifter är de förvaltningsavgifter som du normalt betalar. Fonderna tar vanligtvis 1-3 % per år i förvaltningsavgift. Har du investerat 10 000 kr i en fond med 2 % i förvaltningsavgift betalar du alltså 200 kr per år i förvaltningsavgift.
Ränta på ränta effekten innebär att du inte bara får ränta på dina sparade pengar, du får även ränta på den ränta som genererats under föregående år. Du får helt enkelt ränta på räntan. Effekten fungerar på samma sätt med avkastning från till exempel aktier.
| År | Kronor vid årets början | Avkastning (8 % per år) | Kronor vid årets slut |
| 1 | 200 000 | 16 000 kr | 216 000 |
| 2 | 216 000 | 17 280 kr | 233 280 |
| 3 | 233 280 | 18 662 kr | 251 942 |
| 10 | 399 800 | 31 984 kr | 431 784 |
| 25 | 1 268 233 | 101 459 kr | 1 369 692 |
Tabellen visar resultatet av ränta på ränta effekten vid en årlig ränta eller avkastning på 8%. Formeln nedan visar formeln för ränta på ränta.
Ränta på ränta med aktier, fonder & ränteinkomster
När man räknar så spelar det egentligen ingen roll om man väljer att investera sina pengar i aktier, fonder eller på ett räntekonto. Effekten blir densamma. Det som skiljer är hur stor årsavkastning man får. Aktier och fonder har dock över tid levererat bättre avkastning än ränteplaceringar.
Hela formeln bygger på att man återinvesterar den avkastning som man får varje år. Investerar du pengarna i aktier så återinvesterar du eventuell utdelning som du får varje år, investerar du i fonder så görs återinvesteringarna automatiskt i fonden och på ett räntekonto sker återinvesteringen också automatiskt på kontot.
Varje gång du får någon sorts avkastning utbetald från dina investeringar så skall du alltså återinvestera de pengarna. Då uppnår du ränta på ränta effekten på dina investeringar.
Du kan få ränta-på-ränta effekten även när du investerar i företag/aktier som inte ger någon utdelning. Så länge företaget genererar vinster som återinvesteras i företaget så uppnås effekten den vägen.
Vårt bästa tips: Månadsspara och köp investmentbolaget Investors aktie (köp B-aktien). Utdelningen du får varje år återinvesterar du genom att köpa fler Investor-aktier. Genom att investera i Investor får du en hög avkastning över tid och en stor riskspridning eftersom Investor i sin tur äger många olika företag.
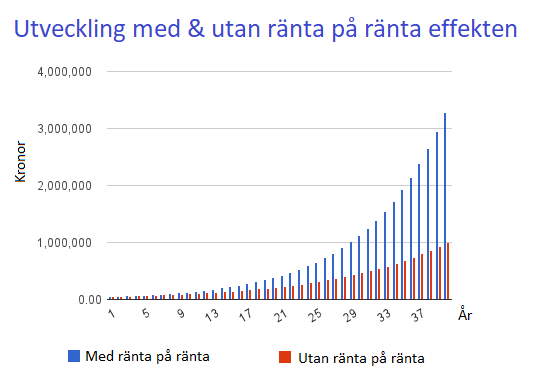
På bilden/grafen ser ni vilken stor skillnad det blir på investeringens utveckling om man återinvesterar räntan eller avkastningen man får. Investeringen ökar mer än 3 gånger så mycket på samma tid tack vare detta fenomen.
Ränta-på-ränta via aktier och fonder
Köp aktier i Investor och handelsbanken exempelvis så får du årlig utdelning. Återinvesterar du utdelningen varje år så skapar du ränta-på-ränta effekten på dina pengar.
Äger du fonder så stannar eventuella utdelningar kvar i fonden och återinvesteras automatiskt vilket innebär att du får ränta på ränta effekten även där.
💡 Erbjudanden – gratis courtage vid aktiehandel!
🔗 Levler.se | Ny svensk nätmäklare med 0 kr i courtage för alla fram till 2025-03-31.
🔗 Avanza.se | 0 kr i courtage & fondavgifter för alla med max 50 000 kr på kontot.
🔗 Nordnet.se | 0 kr i courtage & fondavgifter för alla med max 50 000 kr på kontot.
Dela upp dina pengar på olika nätmäklare för att handla med gratis courtage för en större summa.
Det är gratis att öppna och att ha konto hos alla nätmäklarna ovan.
Gratis courtage:
Courtage är namnet på avgiften som nätmäklarna tar vid köp- och sälj av aktier. Nätmäklarna ovan erbjuder gratis courtage vid aktiehandel vilket innebär att du inte behöver betala någon avgift när du köper och säljer så länge du uppfyller kraven för erbjudandet.
Gratis fondavgifter:
Avanza och Nordnet erbjuder 0 kr i fondavgifter så länge du har max 50 000 kr på kontot. Fondavgifter är de förvaltningsavgifter som du normalt betalar. Fonderna tar vanligtvis 1-3 % per år i förvaltningsavgift. Har du investerat 10 000 kr i en fond med 2 % i förvaltningsavgift betalar du alltså 200 kr per år i förvaltningsavgift.
Agera bank och tjäna pengar på ränta
Följ våra investeringar i Savelend där vi investerat 10 000 kr. Genom deras plattform kan du på ett säkert, roligt och lönsamt sätt investera i lån till andra privatpersoner och företag och tjäna ränteintäkter. Dina pengar sprids ut på massor av olika lån vilket minskar risken rejält. Det är gratis att öppna konto och minsta insättning är 500 kr.
Savelend = Investera i lån till privatpersoner, företag eller investera dom i factoring eller inkassoportföljer.
Se resultatet för våra investeringar
Vi har själva investerat pengar i via plattformarna vi nämner ovan och du kan följa utvecklingen för våra olika investeringar här: https://www.aktiekunskap.nu/strategier/vara-investeringar-utveckling-och-statistik/
Ytterligare förklaring av begreppet ränta-på-ränta
Ränta på ränta, eller compounding som det heter på engelska är ett uttryck som används när man pratar om utvecklingen på investerat kapital. Ränta-på-ränta, som även kallas för sammansatt ränta bygger på att avkastningen varje år beräknas på ditt investerade belopp plus all tidigare avkastning som man erhållit under perioden. Du får alltså avkastning på avkastningen eller du får ränta på räntan.
Detta fenomen gör att kapitalet växer kraftigare ju längre tid man räknar med i formeln. Kurvan över utvecklingen blir helt enkelt brantare och brantare ju längre tiden går
Ränta-på-ränta effekten har av Albert Einstein kallats för ”världens åttonde underverk” och ”den starkaste kraften i universum”.
Hur det beräknas & räkneexempel
Exempel
1000 kr sätts in på ett bankkonto med 5% i ränta.
År 1 får investeraren 5% i ränta på 1000 kr = 1050 kr
År 2 får investeraren 5% i ränta på 1050 kr = 1102,50 kr
År 3 får investeraren 5% i ränta på 1102,5 kr = 1157,625 kr
Efter 3 år så har investeraren ett totalt saldo på 1157,625 kr.
Om man istället väljer att räkna med 15 % i avkastning (dvs utan ränta på ränta efffekten) så blir resultatet istället bara 1150 kr. Det betyder att resultatet blir 7,625 kr (0,66%) bättre efter 3 år med ränta på ränta effekten. Det kan låta lite men ju längre tiden går desto mer påverkar ränta på ränta effekten och det är därför kurvan blir brantare och brantare med tiden.
Efter 20 år med 5% i årlig avkastning får man istället resultatet 2655 kr med ränta på ränta. Räknar man istället med 20 X 5%, dvs 100% i avkastning så blir totalbeloppet bara 2000 kr. Avkastningen blir alltså 32,75% bättre med ränta-på-ränta. Man märker då den kraftiga effekt som ränta-på-ränta ger.
Hur ofta kapitalet dubblas
Om du inte sätter in några extra pengar under åren(du månadssparar inte) utan endast använder ett startkapital och räknar med 10 % i avkastning så fördubblas dina pengar varje 7,2 år. Om du istället räknar med 8 % i årsavkastning så fördubblas dina pengar varje 9 år.
Hej det sklijer sig ganska mycket för beloppet mellan eran hemsida och denna hemsida econello.com/sv/kalkylatorer/rakna-ranta-pa-ranta/. Vet inte vilken man ska utgå efter riktigt. Jag vill räkna ut följande:
Startsumma: 30 000kr
Årsränta: 8%
Sparande i månaden: 5000 kr
Tid: 15år.
Vad skulle detta bli för sparande? Stämmer det med att jag skulle spara ca 360 000 kr?
Hej Jonas
Så här räknar jag ut detta.
1) Du har en startsumma på 30 000 kr, denna kommer att växa i 15 år med räntan 8 %. Den har då vuxit till:
$ 30000\cdot1,08^{15}≈95\,165 $
2) Sedan kan vi beräkna vad ditt månadssparande blir för summa. Du sparar 5000 kr i månaden så du sparar alltså $12\cdot5000=60\,000$ per år. För att räkna ut ränta på ränta effekten av detta sparande så använder vi formeln för en geometrisk talföljd, dvs vi får
$\frac{60000\cdot(1-1,08^{15})}{1-1,08}≈1\,629\,127\,kr$
Tänk på att en ökning med 8 % betyder en förändringsfaktor 1,08
När vi lägger ihop dessa bägge summor får jag $1\,629\,127+95\,165=1\,724\,292\,kr$
Hejsan!
Jag är helt novis på detta. Om jag vill ”spara” enligt din kalklyl. Vad behöver jag göra då? Ska jag investera i en aktie? aktiefond? räntefond?
Du ska tänka att behöver veta exakt vad som jag ska göra. Jag förstår inte hur jag ska påbörja sparandet.
Tack på förhand!
Hej!
Det är svårt att ge ett generellt svar vad du skall börja med att investera. Kika gärna vidare här på sajten och lär dig mer om aktier, aktiefonder och räntefonder. Det är ett bra första steg för att veta hur du skall börja att spara. Då lär du dig mer om olika alternativ och vad som eventuellt kan passa dig.
Hoppas att detta råd hjälper dig framåt! Annars får du fråga mer 🙂
Detta med ränta på ränta konton existerar inte i verkligheten, Annars skulle ju alla bolag marknadsföra detta med ett färdigt koncept.
Att tänka sig 10% ränta är ju snyggt men vart finns konton som erbjuder detta, Just dessa frågor var det ju det som Anna-Karin frågande om.
Att vilseleda människor är ganska syniskt.
Senast idag 2019-05-13 så körde TV1 en deal med ränta på ränta som Norén berättade, Han kunde sedan inte svara på frågan om HUR?
Börjar man vid 20år och sparar 1000/mån och sparar i 45 år.
Sparande – avkastning idag sker på År inte per månad.
1000 *12 = 12000 per år.
12000 * 10år = 120000
120000 * 10år =1200000
1200000* 10år =12000000
12000000* 10år =120000000
Vilket gör att det är enligt räkneexemplen ett konto med 120 Miljoner?
Man skulle vilja veta VAR detta konto finns?
Knappast hos den statliga pensionmyndigheten.
Den normala pensionen idag alltså den statliga ligger på ca 2.5 miljoner som ska räcka i 30 År.
men men vh JP
Hej
Nej med sparkonton så är det omöjligt att få sådan ränta. Det finns förvisso sparkonton med ränta uppåt 6 % men som inte omfattas av insättningsgaranti och som har begränsningar på hur mycket som får sättas in. Däremot så kan du säkerligen uppnå en ränta på ränta effekt på cirka 9-11 % om du investerar klokt i aktier över lång tid. Det kräver förstås mer aktivitet och intresse. Börsen har ju historiskt gått upp i snitt med cirka 9-11 % per år.
Förstår mig inte riktigt på räkneexemplet från JP ovan.
Om man sparar 1000 kr/månaden i 45år borde man väl hamna på..
Utan ränta: 540 000 kr
Med 10% årsränta: 8 626 858 kr
Sparande/
År Månad Månader Sparande/år Totalt utan ränta Totalt med ränta
1 1 000 kr 12 12 000 kr 12 000 kr
2 1 000 kr 12 12 000 kr 24 000 kr 25 200 kr
3 1 000 kr 12 12 000 kr 36 000 kr 39 720 kr
4 1 000 kr 12 12 000 kr 48 000 kr 55 692 kr
5 1 000 kr 12 12 000 kr 60 000 kr 73 261 kr
6 1 000 kr 12 12 000 kr 72 000 kr 92 587 kr
7 1 000 kr 12 12 000 kr 84 000 kr 113 846 kr
8 1 000 kr 12 12 000 kr 96 000 kr 137 231 kr
9 1 000 kr 12 12 000 kr 108 000 kr 162 954 kr
10 1 000 kr 12 12 000 kr 120 000 kr 191 249 kr
20 1 000 kr 12 12 000 kr 240 000 kr 687 300 kr
30 1 000 kr 12 12 000 kr 360 000 kr 1 973 928 kr
40 1 000 kr 12 12 000 kr 480 000 kr 5 311 111 kr
45 1 000 kr 12 12 000 kr 540 000 kr 8 626 858 kr
Nej beräkningarna där verkar inte stämma.
Om du skall räkna med en ränta-på-ränta effekt så behöver man använda en formel för geometriska talföljder. Se faktainformation ovan.
Om jag startar med 4 000 000 kr o räknar med en 5% uppgång över tid i fonder jag. Varje år tar jag ut 150 000 kr av räntan. Hur ser utvecklingen ut över 20 år.
Mvh Anders
Hej Anders.
Det får du räkna ut själv.
Mvh admin på Aktiekunskap